OBB에 대한 이해 및 설명.(SAT, Saperating Axis Theorem)

일반적으로 충돌에 관한 알고리즘은 크게 AABB, OBB 그리고 circle 로 나누어집니다. (외국사이트에서는 OBB라는 단어보단, SAT Seperating Axis Theorem라는 말로 더 언급이됩니다.) 일단 AABB는 직사각형의 LT RB의 주소를 파악한다음 계산하는거라 속도및 연산이 빠르지만, Rotation에 무방비해보입니다. OBB의 원리에 대한 일반적인 이해를 돕고자 이 글을 쓰게 되었습니다. 

 

OBB설명 (아직 타이핑이 익숙하질 않아서 노트로 정리를 해보았습니다 ^^;;)

일단 OBB의 관한 설명은 다음의 사이트에서 참조하면 좋습니다. 

http://www.gingaminga.com/Data/Note/oriented_bounding_boxes/#4._%EC%B0%B8%EA%B3%A0_%EB%AC%B8%ED%97%8C" target="_blank" rel="noopener" data-mce-href="http:// http://www.gingaminga.com/Data/Note/oriented_bounding_boxes/#4._%EC%B0%B8%EA%B3%A0_%EB%AC%B8%ED%97%8C">http:// http://www.gingaminga.com/Data/Note/oriented_bounding_boxes/#4._%EC%B0%B8%EA%B3%A0_%EB%AC%B8%ED%97%8C 

Object Oriented Bounding Box 를 이용한 Collision Detection

위에 url를 보면 OBB는 실제로 수학적 계산이 쉽다는 것을 설명합니다. 하지만, 그 계산에서 빼먹은 것이 종종있기때문에, 각각부분에서의 추가설명을 하도록 하겠습니다.

 

 

 

 

 

 

위에식 에서, 전개에 대한 설명을 하자면,

 

왼쪽식이 오른쪽 첫번째 식으로 넘어갈 수 있는 근거는 외적의 삼중곱 성질에 의해 설명이 가능합니다(삼중곱은 네이버에)

 

오른쪽의 첫번째식이 두번째식으로 변환 가능한 이유는 A1, A2, A3는 서로 수직인 basis로 정해놓았기 때문에 어떤 두 단위 벡터의 외적은 자연스럽게 나머지 한 백터가 됩니다.

 

오른쪽의 두번째식이 세번째 식으로 넘어가는 과정은 우리가 저 사이트에서의 가정이 A1, A2, A3를 각각 basis로 변환을 한다음 Transformation과 Rotation을 사용하기로 했으므로. B2벡터의 3번째원소가 되는것입니다. (basis로 변환했다는 이야기는, 간단하게 A1 을 (1,0,0)으로 바꾸고 A2를 (0,1,0)으로 바꾸고 A3를 (0,0,1)로 정해놓고 좌표계를 다시 바꾸겠다는 뜻입니다. 사실 Ai는 단위벡터(=길이가 1) 이므로 변환에 큰 절차가 필요가 없습니다.

 

마지막으로 basis가 A1, A2, A3에서 rotation Matrix R은 사실 (1,0,0) 이 B1, (0,1,0)이 B2 , (0, 0, 1)이 B3로 바꿔준다는 이야기기 때문에 R의 열벡터들 ( 세로로 자른애들) 은 각각 B1, B2, B3가 됩니다. 따라서 R32 는 행렬 R의 3행 2열이므로 B2의 세번째원소과 같은것이 됩니다. 따라서 저식은 주어진 조건내에서 성립이 됩니다.

 

 

T*L이 왜 부등식의 왼쪽항이 되는 이유는

우리는 L = A1 X B2 라고 축을 정해놓았는데, B2 = R*A2 라고 할 수있고, 이는 곧

 

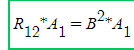
이렇게 됩니다 마찬가지로

 

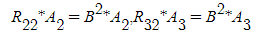
라고 할 수 있습니다.

이를 A1과 외적을하면 분배법칙에 의해서

 

 

 

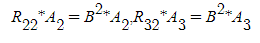
가됩니다. 여기에 T를 내적으로 곱해주면 부등식의 왼쪽과 같은 식이 나오게 됩니다.

 

따라서 우리가 직육면체에 대한 실질적 OBB Axis Check는 다음표의 식들만 계산을 하면 됩니다.

 

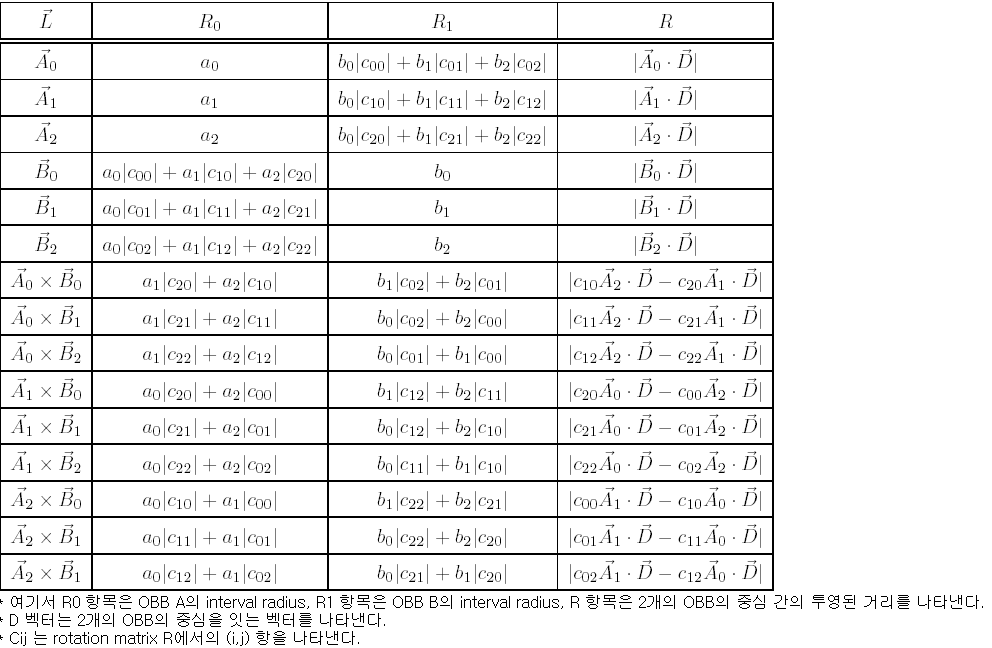
왜 SAT이론 에서 두 볼록다면체가 떨어지기 위한 필요충분조건이 각면의 법선벡터 및 두 도형의 모서리의 외적을 축으로 하면서 사영을해야하는지에 대한 증명은 다음에 시간적여유가 되면 해보도록 하겠습니다.

 

http://www.gingaminga.com/Data/Note/oriented_bounding_boxes/obb-tree.pdf 참조하시면 도움은 됩니다.